Union find 문제란?
Union find 문제는 같은 그래프로 묶을 수 있는 노드끼리 구별하는 문제입니다.
예를 들어 노드가 아래와 같이 연결되어 있다고 가정합니다.
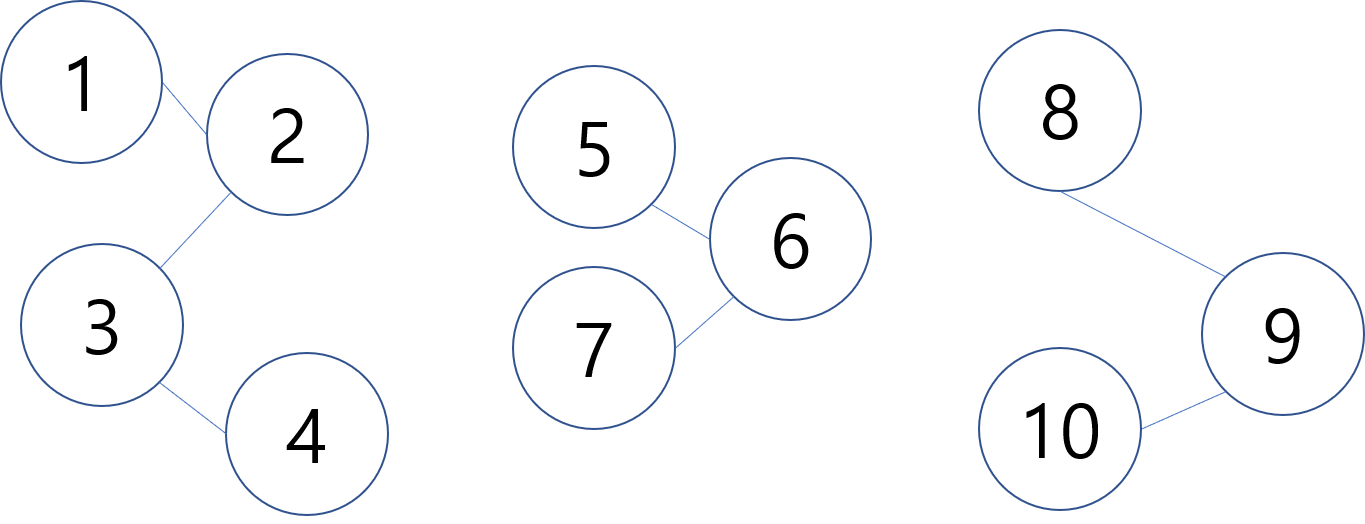
노드간의 관계를 출발->목적지로 표현한 list로 정의합니다.
# 방향성 없는 노드
nodes = [ [1,2], [2,3], [3,4], [5,6], [6,7], [8,9], [9,10] ]
여기서 union find 문제를 풀기 위해 총 3개의 함수를 정의합니다.
- union_find
- getParent
- union_parent
해답 코드
class unionset:
def __init__(self, numnodes):
self.parent = []
for i in range(numnodes+1):
self.parent.append(i)
def getParent(self, node):
if self.parent[node] == node:
return node
else:
return self.getParent(self.parent[node])
def union_parent(self, node1, node2):
if node1 < node2:
self.parent[node2] = node1
else:
self.parent[node1] = node2
def union_find(self, nodes):
for i in range(len(nodes)):
self.union_parent(self.getParent(
nodes[i][0]), self.getParent(nodes[i][1]))
먼저 본 함수인 union_find를 정의합니다. 먼저 자기 자신의 번호로 자신의 부모 노드를 초기화하기 위해서 노드 개수+1만큼의 리스트를 선언해줍니다. 그래야 인덱스1에 1번 노드의 부모 정보가 입력됩니다.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
그 결과는 위 표와 같습니다. 그 다음, 주어진 노드와 간선을 이용하여 부모 노드를 정해줍니다.
getParent 함수는 부모가 자기 자신이라면 자신을 리턴하고, 아닌 경우에는 부모 노드의 부모를 구해 리턴합니다. union_parent 함수는 두 노드를 받아 더 작은 숫자를 부모로 리턴합니다.
# 방향성 있는 노드
nodes = [ [1,2], [2,3], [3,4], [5,6], [6,7], [8,9], [9,10] ]
union_parent 함수는 nodes 리스트 중 1번째 원소인 [1,2]를 입력으로 받게 됩니다. 따라서 getParent(1,parent)와 getParent(2, parent)를 비교하여 작은 값을 리턴합니다. 여기서 getParent(1,parent)는 1이고, getParent(2,parent) 2이므로 parent[2] = 1이 됩니다.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 1 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
마찬가지 방식으로 반복한 결과, 부모 노드는 아래와 같이 됩니다.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 1 | 1 | 1 | 5 | 5 | 5 | 8 | 8 | 8 |

![[Python] 합집합 찾기 Union find / Disjoint-set 문제](https://images.unsplash.com/photo-1537498425277-c283d32ef9db?ixlib=rb-1.2.1&q=80&fm=jpg&crop=entropy&cs=tinysrgb&fit=max&ixid=eyJhcHBfaWQiOjExNzczfQ&w=2000)