![[Python] 정렬 알고리즘 정리(버블, 카운팅, 선택, 퀵, 삽입, 병합, 힙)](https://images.unsplash.com/photo-1593642632823-8f785ba67e45?ixlib=rb-1.2.1&q=80&fm=jpg&crop=entropy&cs=tinysrgb&fit=max&ixid=eyJhcHBfaWQiOjExNzczfQ&w=2000)
코딩 테스트에 필수적인 지식인 정렬 알고리즘의 코드와 시간 복잡도를 정리해보려고 한다. 파이썬으로 작성되어 있으며 버블, 카운팅, 선택, 퀵, 삽입, 병합 정렬을 순서대로 설명한다.
개인적인 공부를 위해 정리한 것이므로 틀린 부분이 있을 수 있습니다.
시간 복잡도와 알고리즘 기법
| 알고리즘 | 평균 시간 복잡도 | 최악 시간 복잡도 | 기법 | 비고 |
|---|---|---|---|---|
| 버블 정렬 | $O(n^2)$ | $O(n^2)$ | 비교와 교환 | 구현이 가장 쉬움 |
| 카운팅 정렬 | $O(n+k)$ | $O(n+k)$ | 비교환 방식 | n이 작을 때 유리함 |
| 선택 정렬 | $O(n^2)$ | $O(n^2)$ | 비교와 교환 | 교환 회수가 버블, 삽입정렬보다 작음 |
| 퀵 정렬 | $O(n \log n)$ | $O(n^2)$ | 분할 정복 | 평균적으로 가장 빠름 |
| 삽입 정렬 | $O(n^2)$ | $O(n^2)$ | 비교와 교환 | n이 작을 때 유리함 |
| 병합 정렬 | $O(n \log n)$ | $O(n \log n)$ | 분할 정복 | 연결 List의 경우 가장 효율적인 방법 |
버블 정렬(Bubble Sort)
작은 값과 큰 값이 순서를 바꾸며 큰 값이 제일 뒤로 이동하는 모습이 거품이 떠오르는 모양과 같다 해서 붙여진 이름이다.
def bubblesort(arr):
temp = 0
for i in range(len(arr)):
for j in range(len(arr)-i-1):
if arr[j] > arr[j+1]:
temp = arr[j]
arr[j] = arr[j+1]
arr[j+1] = temp
return arr
arr = [5, 6, 2, 1, 4, 3]
print(bubblesort(arr))
카운팅 정렬(Counting Sort)
카운팅 정렬은 배열 원소의 등장 횟수를 세어서(Counting) 정렬하는 방식이다. 주어진 배열 원소의 값이 작을 때는 매우 빠르지만, 원소의 값이 클 경우에는 매우 비효율적이다.
def countingsort(arr):
# 만일 배열의 최대값을 쉽게 구할 수 없다면 소요 시간은 더 늘어남
repo = [0] * (max(arr)+1)
# 원소 등장 횟수 카운팅
for i in range(len(arr)):
repo[arr[i]] += 1
arrtemp = []
for i in range(len(repo)):
for j in range(repo[i]):
arrtemp.append(i)
arr = arrtemp
return arr
arr = [2, 1, 1, 4, 4, 4, 4, 3, 2, 2]
print(countingsort(arr))
선택 정렬(Selection Sort)
주어진 배열에서 최소값을 먼저 찾은 후, 그 최소값을 배열의 맨 앞으로 보낸다. 그 다음 정렬되지 않은 나머지 부분에 대해서 이를 반복하는 방법이다.
def selectionsort(arr):
for i in range(len(arr)):
minInd = i # 최소값을 저장하는 인덱스
temp = 0
for j in range(i, len(arr)):
if arr[minInd] > arr[j]:
minInd = j
temp = arr[i]
arr[i] = arr[minInd]
arr[minInd] = temp
return arr
arr = [5, 6, 2, 1, 4, 3]
print(selectionsort(arr))
퀵 정렬(Quick Sort)
퀵 정렬은 분할 정복(Divide and conquer)방식으로 정렬을 수행하는데, 평균 수행 속도가 빠르기 때문에 가장 많이 쓰이는 정렬 알고리즘 중 하나이다. 기준점은 배열의 시작이나 끝 또는 중간값을 선택하기도 하지만 랜덤으로 정하기도 한다. 수행 순서는 다음과 같다.
- 기준점(Pivot point)을 설정한다.
- 주어진 배열의 시작과 끝을 변수
start와end에 저장한다. while문에서 Pivot point보다 크면 오른쪽으로, 작으면 왼쪽으로 이동시킨다.start와end변수의 값을 바꾸어준다. 1~3을start<end를 만족할 때까지 반복한다.start와pivot의 값을 바꾸어준다.pivotsort()함수를 재귀함수로 호출하여 반복한다.
예제 코드에서는 배열 시작을 기준점으로 잡아 정렬을 수행한다.
def quicksort(arr, start, end):
pivot = arr[start]
left, right = start, end
while(start < end):
# pivot보다 큰 값을 찾는다
while(pivot <= arr[end] and start < end):
end -= 1
# pivot보다 작은 값을 찾는다
while(pivot >= arr[start] and start < end):
start += 1
# 두 값을 바꿔 줌
arr[start], arr[end] = arr[end], arr[start]
# 0~start는 pivot보다 작고, start+1~end까지는 pivot보다 크다
# 따라서 pivot 위치를 바꾸어 줌
arr[left], arr[start] = arr[start], arr[left]
# pivot의 좌측과 우측에 대해서 다시 정렬
if(left < start):
quicksort(arr, left, start-1)
if(right > end):
quicksort(arr, end+1, right)
return arr
arr = [3, 4, 2, 1, 5, 6]
print(quicksort(arr, 0, len(arr)-1))
예제 arr = [3, 4, 2, 1, 5, 6]로 설명해보자.
pivot==3이다.while문에 진입한 다음 첫 번째while문에서는 오른쪽에서pivot보다 큰 값은 순서대로6, 5이므로end==3이다.- 두 번째
while에서는 바로 4가 나타나기 때문에pivot보다 작은 값은 없다. 따라서start==1이다. - 두 인덱스에 맞추어 값을 바꾼다. 따라서 4와 1이 바뀌어
arr = [3, 1, 2, 4, 5, 6]이다. - 2~4를 반복한다.
pivot을arr[start]와 바꾸어 준다.pivot기준으로 좌측과 우측에 대해서 재정렬한다.
삽입 정렬(Insertion Sort)
삽입 정렬은 현재 인덱스를 기준으로 앞의 원소들과 비교해 적절한 위치에 현재 인덱스의 값을 삽입하는 정렬 방법이다.
def insertionsort(arr):
for i in range(1, len(arr)):
for j in range(len(arr[0:i])):
if arr[j] > arr[i]:
arr[i], arr[j] = arr[j], arr[i]
return arr
arr = [5, 6, 2, 1, 4, 3]
print(insertionsort(arr))
병합 정렬(Merge Sort)
병합 정렬은 주어진 데이터를 반으로 나누어(Divide) 나누어진 리스트를 정렬(Conquer)한 다음 병합(Merge)하는 방식으로 이루어진다.
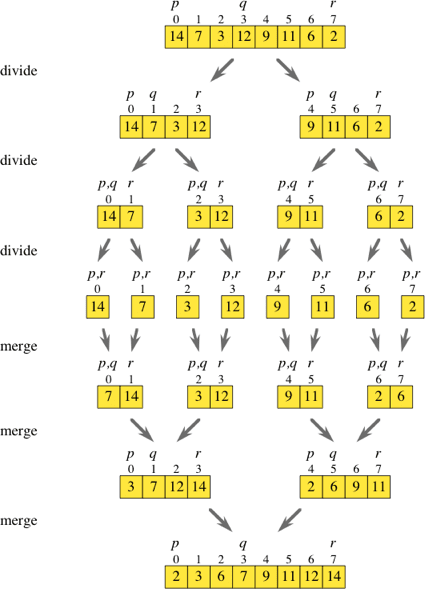
예제 코드는 리스트를 분할하는 부분과 합치는 부분으로 나누어져 있다. 먼저 mergesort에서 각 리스트를 1개 단위로 나누어질 때까지 분할하고, merge를 통해 합치면서 정렬한다. 이 과정을 반복해서 최종적으로 정렬된 리스트를 얻게 된다.
def merge(left, right):
lenl, lenr = len(left), len(right)
result = [0]*(lenl + lenr)
i=j=k=0
while lenl > i and lenr > j:
if left[i] < right[j]:
result[k] = left[i]
i+=1
else:
result[k] = right[j]
j+=1
k+=1
result[k:] = right[j:] if lenl-i<lenr-j else left[i:]
return result
def mergesort(arr):
if len(arr) <= 1:
return arr
middle = len(arr)//2
leftlist = arr[:middle]
rightlist = arr[middle:]
leftlist = mergesort(leftlist)
rightlist = mergesort(rightlist)
return merge(leftlist, rightlist)
arr = [3, 4, 2, 1, 5, 6]
print(mergesort(arr))
병합 정렬은 시간 복잡도가 #O(n log n)#로 보장되기 때문에 강력한 알고리즘이다. 하지만 재귀함수 호출 깊이가 배열의 크기에 따라서 늘어나기 때문에 메모리를 너무 많이 소모하는 단점이 있다. 이 다음에 소개할 힙 정렬은 이런 메모리 관리 문제를 해결했다.
힙 정렬(Heap Sort)
힙 정렬은 이진 트리를 이용한 정렬 방법이다. 이를 이해하려면 먼저 힙 구조, 정확히는 최대 힙 구조를 이해해야 한다. 최대 힙 구조란 부모가 자식보다 값이 큰 이진 트리이다.
먼저 임의의 배열 arr = [3, 4, 2, 1, 5, 6]을 힙 구조로 배열한다. 그러면 가장 위의 root에는 배열의 최대값이 위치한다. 이를 힙 구조의 맨 마지막 값과 바꾸어주고, 맨 마지막 값을 제외한 나머지 부분에 대해서 다시 힙 구조화(heapify)를 수행한다. 이를 모든 원소에 대해서 반복해주면 전체 원소가 정렬된다.
첫 번째 방법
첫 번째 방법은 힙 모듈을 사용하지 않고 최대 힙을 구현하는 방식이다.
def heapify(arr):
for i in range(len(arr)):
child = i
while(child != 0):
root = (child-1)//2
if arr[root] < arr[child]:
arr[child], arr[root] = arr[root], arr[child]
child = root
return arr
def heapsort(arr):
arr = heapify(arr)
for i in range(len(arr)):
arr[len(arr)-(i+1)], arr[0] = arr[0], arr[len(arr)-(i+1)]
arr[:len(arr)-(i+1)] = heapify(arr[:len(arr)-(i+1)])
return arr
arr = [3, 4, 2, 1, 5, 6]
print(heapsort(arr))
두 번째 방법
두 번째 방법은 heapq모듈을 사용하는 방식이다. heapq모듈은 최소 힙을 만들어주는데, heappop()을 사용해 가장 작은 원소부터 꺼내주면 정렬이 완성된다.
import heapq
def heapsort(arr):
heap = []
for ele in arr:
heapq.heappush(heap, ele)
sortedarr = []
while heap:
sortedarr.append(heapq.heappop(heap))
return sortedarr
arr = [3, 4, 2, 1, 5, 6]
print(heapsort(arr))