01-Probability and Random Variables: A Review (1/5)

랜덤 신호와 관련된 확률론과 랜덤변수, 그리고 칼만 필터링에 대해서 차근차근 정리해보려고 한다. 기본적인 부분인데도 디테일한 부분은 잘 기억나지 않는 경우가 종종 있다. 한번 쭉 정리해놓으면 나중에 찾아서 보기도 편하고, 한국어로 정리된 자료가 없는 것 같아서 직접 정리해 보고자 한다.

오늘은 공리적 확률과 랜덤변수에 대해서 다뤄보고자 한다.

공리적 확률(Axiomatic probability)

직관적인 확률 정의는 한계가 뚜렷하다. 모든 경우가 같은 확률을 가지는 것은 대부분 상황에 적합하지만, 때로는 "불공평한" 확률이 필요한 경우가 있다.

공리적 확률을 정의하기 위해서는 표본 공간(Sample space)이라는 개념을 알아야 한다. 예를 들어 주사위 던지기를 하는 경우, 표본공간은 1부터 6까지의 나올 수 있는 모든 눈이다. 각 결과값(outcome)은 표본공간상의 원소(Elements)또는 점(Point)라고 불린다. 앞으로 표본공간은 $S$, 그리고 원소의 집합은 ${s_1, s_2, \cdots}$라고 표기한다.

여기서 중요한 사실은 표본공간 안의 원소들은 상호배타적(mutually exclusive or disjoint)이어야 한다는 점이다. 예를 들어 주사위를 던져서 나오는 결과는 1부터 6까지 총 6가지로 서로 중복되지 않는다.

공리적 확률에서 '사건(event)'이라는 단어는 특별한 의미를 가지고 있다. 그리고 '결과'와 혼동하지 말아야 한다. 사건은 표본공간의 특정 부분집합을 의미한다. 표본공간에서 정의되는 여러 사건들은 대문자로 $A, B, C, \cdots$또는 $A_1, A_2, \cdots$와 같이 나타낸다.

다음으로는 공리적 확률의 3가지 공리에 대해 알아보자.

$$
\text{공리 1: }P(A)\geq0\
\text{공리 2: }P(S)=1
$$

모든 확률값은 0보다 크거나 같고, 표본공간상의 모든 사건이 일어날 확률은 1이다. 이제 $A_1, A_2, \cdots$를 표본공간상의 상호배타적인 사건들이라고 하자.

$$
\begin{aligned}
\text{공리 3: }&P(A_1 \cup A_2 \cup A_3 \cup \cdots)\\\ &= P(A_1)+P(A_2)+P(A_3)+\cdots
\end{aligned}
$$

각 사건의 합집합의 확률은 각 사건의 확률의 합과 같다. 하지만 아래 벤 다이어그램과 같은 경우에는 조금 다른 결과가 나온다.

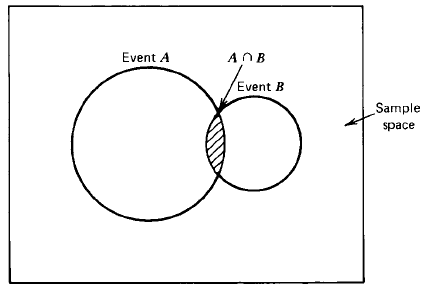
이 경우에는 사건 A, B에 공통인 부분이 있다. 따라서
$$
P(A\cup B)=P(A)+P(B)-P(A\cap B)
$$
와 같이 나타난다. $P(A\cap B)$는 Joint Probability라고 부른다. 자세한 내용은 뒤에서 설명하겠다.

랜덤 변수(Random Variables)

실제로 노이즈가 섞인 신호를 다루다 보면, 우리가 접하는 것들은 신호의 전압(Volt), 힘(N), 거리(m)와 같은 물리량들이다. 이는 주사위의 눈처럼 실체적 객체가 있는 것들이다. 따라서 이런 객체들의 확률을 다루기 위해서 랜덤 변수(Random variable)라는 개념을 도입하게 된다.

예를 들어, 어떤 표본공간이 존재하고 각 사건에 해당하는 확률이 있다고 가정하자. 이때 확률변수란, 단순하게 표본공간상의 각 원소를 실선 상의 한 점으로 매핑(mapping)하는 역할을 한다.

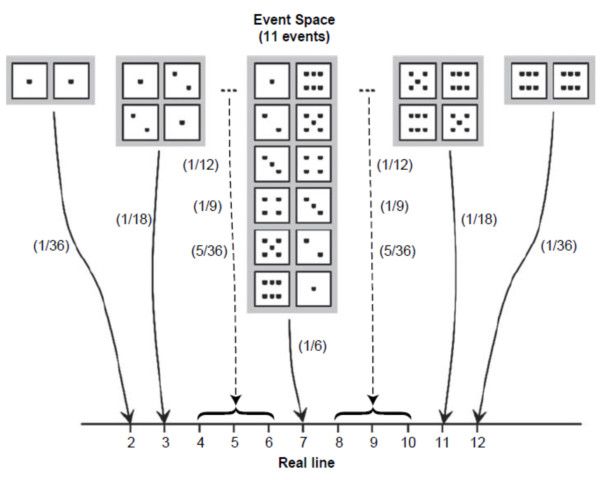
위 그림은 주사위 두 개를 던지는 경우에 대한 표본공간의 각 사건을 실선상에 매핑한 결과를 나타내고 있다. 주사위 두개의 눈금의 합은 1부터 12로 나타나는 실체적 객체를 지니고 있기 때문에 위와 같은 표현이 가능하다. 참고로 위 그림에서 괄호 한의 숫자는 각 사건이 발생할 확률을 나타낸다.

Joint 확률, 조건부 확률(Conditional Probability)

이번 섹션부터는 베이즈 확률론에서 굉장히 중요한 개념들이 많이 나온다. 특히 Joint 확률과 조건부 확률은 베이즈 법칙의 토대를 이루는 부분이기 때문에 확실하게 이해하는 것이 중요하다. 나중에 필터링에 넘어가면 이 부분이 정말 많이 응용된다.

실제 환경에서는 여러 확률적 환경을 고려해야 하는 경우가 대부분이다. 예를 들어, 1부터 13이 적힌 카드 중에서 한 장을 뽑는 게임을 생각해보자. 이때 랜덤 변수는 카드에 적힌 숫자가 된다.

왜 랜덤 변수가 카드에 적힌 숫자인지 이해가 되지 않으면 확률론과 랜덤변수 1편을 보고오자.

카드 한 장을 뽑아 적힌 숫자를 기록하고, 다시 넣고 섞은 다음 새롭게 한 장을 뽑아서 숫자를 기록한다. 이때 처음 기록한 숫자를 X, 두번째로 기록한 숫자를 Y라고 하자. 이 과정을 통계적으로 유의미한 정도의 횟수를 반복한다. 이제 X, Y를 랜덤변수라고 부를 수 있다.

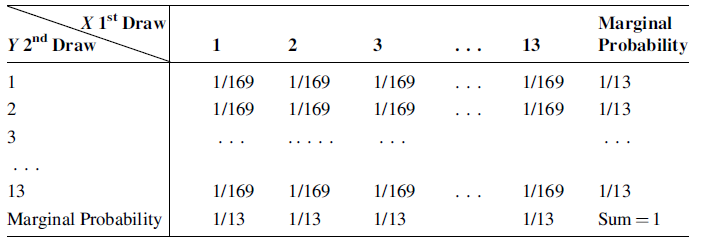
각 경우에 대한 확률을 정리하면 위 표와 같다. 처음 뽑은 카드를 다시 카드 뭉치에 넣고 섞은 다음 두번째 카드를 섞었기 때문에 첫번째 사건과 두번째 사건은 당연하게도 독립이다. 위 표를 보면 처음에 어떤 숫자를 뽑던지 간에 두번째 뽑는 숫자에 미치는 영향이 없음을 확인할 수 있다.

이제 우리는 X, Y를 함께 묶어 새로운 표본공간을 정의할 수 있다. X와 Y가 joint된다는 의미에서 이를 Joint probability라고 부르고, $p_{XY}$로 표현한다. 위 표를 다시 보면 확률은 모두 0 이상이고, 각 행에 대해 합하거나, 열에 대해서 합하거나 확률의 합은 모두 1이다. 따라서 $P_{XY}$는 공리 1,2를 만족하므로 공리적 확률임을 알 수 있다. 이때 각 행과 열은 어느 한 쪽이 고정된 상태로 나머지 랜덤변수에 대해 확률의 합을 계산한 것인데, 이를 Marginal probability라고 부른다. 다시 말해서, X, Y중 하나가 어떤 값을 가지는 경우, 나머지 하나의 확률은 상대적으로 나타난다는 것이다. 예를 들어, 첫번째 행은 Y=1인 경우이다. 이때 X가 어떤 숫자가 나오던지 Y가 나올 확률은 1/13이다.
$$
p_Y=\frac{1}{13}=\frac{1}{169}+\frac{1}{169}+\cdots+\frac{1}{169}
$$
다음으로 조건부 확률(Conditional probability)에 대해서 알아보자. 이번에는 X나 Y중 하나가 특정 값이 나오는 조건에서, 나머지 랜덤변수가 특정 값을 가질 확률을 계산해보자. 예를 들면 X=3일때, Y=2일 확률은 위 표에 따르면 1/169이다. 이를 수식으로 나타내면
$$
P_{Y=2|X=3}=\frac{1}{169}
$$
와 같다.

베이즈 법칙(Bayes Rule)

베이즈 법칙은 다음과 같다. 식에 대한 자세한 설명은 나중에 나오니 지금은 식의 모양만 눈에 익혀두자.
$$
P_{X|Y}=\dfrac{P_{Y|X}P_X}{P_Y}
$$
베이즈 법칙으로부터 조건부 확률과 Joint 확률간의 관계는 다음과 같이 얻을 수 있다.
$$
P_{X|Y}=\dfrac{P_{XY}}{P_Y}\
P_{Y|X}=\dfrac{P_{XY}}{P_X}
$$
식을 자세히 들여다보면 확률 $P_X, P_Y$가 $P_{XY}$를 정규화(Normalize)하고 있는 것을 볼 수 있다. 이 부분이 직관적으로 이해하기 어려울 수 있는데, X, Y가 동시에 일어나는 사건에서 X, Y 둘 중 하나만 일어나는 경우로 나누어 준다고 생각하면 된다.

독립(Independence)

랜덤변수 X, Y는
$$
P_{XY}=P_X P_Y
$$
를 만족하는 경우 서로 독립이라고 한다. 이는 필요충분조건으로, X, Y가 독립이면 위 식을 만족하고, 위 식을 만족한다면 X, Y는 독립이라고 할 수 있다.

출처

• 그림 출처 : Brown and Hwang, Introduction to random signals and applied Kalman filtering,4th edition

출처

• 그림 출처 : Brown and Hwang, Introduction to random signals and applied Kalman filtering,4th edition