01-Probability and Random Variables: A Review (5/5)

극한(Limits), 수렴(Convergence), Unbiased estimators

어떤 확률 변수 ${Y_n}$을 생각해 보자.
$$
\begin{aligned}
Y_1&=X_1\\\
Y_2&=\frac{X_1+X_2}{2}\\\
Y_3&=\frac{X_1+X_2+X_3}{3}\\\
&\vdots\\\
Y_n&=\frac{X_1+X_2+\cdots+X_n}{n}\\\
\end{aligned}
$$
당연하게도 $Y_n$은 확률변수 $X$의 표본평균(Sample mean)이다. $n$이 커질수록 실제 $X$의 평균에 가까워질 것이라고 예측할 수 있다. 그런데 문제는 얼만큼 많이 표본을 더해야 실제 평균에 가까워질 것인가이다. $X_n$은 말 그대로 표본이라 실제 평균과 차이가 큰 값이 더해질수도, 평균과 비슷한 값이 더해질수도 있기 때문이다.

$X$가 평균 $m_X$에 분산 $\sigma_X^2$를 가진다고 할 때, $Y_n$의 평균은 다음과 같다.
$$
\begin{aligned}
E[Y_n]&=E\left(\frac{X_1+X_2+\cdots+X_n}{n}\right)\\\
&=\frac{1}{n}\big( E[X_1]+E[X_2]+\cdots+E[X_n]\big)\\\
&=\frac{1}{n}\big( nE[X]\big)=m_X
\end{aligned}
$$
먼저 $Y_n$의 기댓값은 표본평균의 평균이므로 $X$의 평균과 같다. 이런 성질을 가지고 있는 Estimator를 Unbiased Estimator라고 부른다.
$$
E[\text{Estimate of }X]=E[X]
$$
$Y_n$의 분산은 다음과 같다.
$$
\begin{aligned}
Var[Y_n]&=E\big[Y_n-E[Y_n]\big]^2\\\
&=E\Big[Y_n^2-2Y_nm_x+m_x^2\Big]\\\
&=E[Y_n^2]-m_X^2\\\
&=E\big[\frac{(X_1^2+X_2^2+\cdots+X_n^2)+2(X_1X_2+\cdots X_{n-1}X_n)}{n^2}\big]-m_X^2\\\
&=\frac{1}{n^2}( nE[X^2]+n(n-1)m_X^2)-m_X^2\\\
&=\frac{1}{n}E[X^2]-\frac{1}{n}m_X^2\\\
&=\frac{1}{n}Var[X]\\\
&=\frac{\sigma_X^2}{n}
\end{aligned}
$$

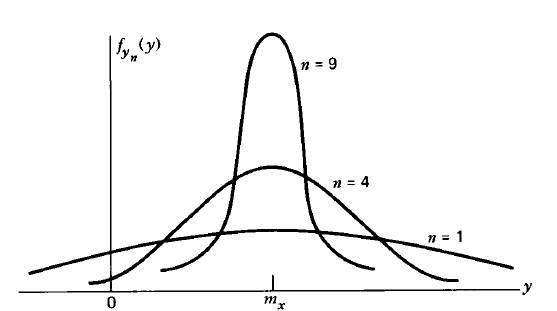
당연하지만 n이 커질수록 확률밀도함수의 그래프는 정규분포를 닮아간다. 평균은 변하지 않지만 분산이 점점 작아지기 때문이다. 또한 그래프 양쪽의 꼬리(tail) 부분 역시 점점 0에 가까워지는 점도 참고하자.

참고 - 추정(Estimation)과 필터링(Filtering)

반복된 시도로부터 파라미터를 추정하는 것은 필터링 문제가 아닌 통계적 접근 방법이다. 필터링 문제에서는 보통 핵심적인 통계적 파라미터를 설정해 놓고, 랜덤 프로세스(Random process)의 시간에 따른 변화를 추정한다. 칼만 필터는 상태변수공간(State Space)안의 상태변수의 시간적 변화를 관찰하는 방법인데, 따라서 필터링은 통계적인 접근법과는 다르다.

그렇지만 필터링 문제에서도 통계적 관점을 일부 취하고 있다.

사실 이 부분이 무슨 뜻인지 잘 모르겠음..

1. 선형 추정(Linear estimate). 확률변수의 선형 추정이란, 측정치의 시간에 따른 선형 함수 형태를 말한다. 과거의 추정치가 현재에도 포함돼 있을 수 있다면 선형적으로 고려되어야 한다는 뜻이다.
2. Unbiased estimate. 위에서 다루었듯이, $E\left[\hat{x}\right]=x$를 만족하는 경우이다.
3. MMSE(Minimum mean square error) Estimator. 오차 $E\left[(x-\hat{x})^2\right]$를 최소화하는 방법이다.
4. Minimum Variance estimate. 분산을 최소로 만드는 방법.
5. Consistent estimate. Dynamic random process를 추정하는 경우, Consistent estimate는 추정 오차가 평균은 0이고 공분산은 필터 계산 결과와 일치하는 경우이다.